Understanding Decibels
Imagine yourself at a dinner party. Some guy
says to you, "I think this wine is 10dB better than the last one." You probably
think that he’s had quite enough already and doesn’t know what he’s talking
about. But he probably does.
The basics
The decibel (dB) is poorly understood by most
audiophiles and a great many people in the audio industry, but it’s really a simple
concept. When most people see "dB," they think of sound-pressure levels. While a
sound-pressure level can be expressed in decibels, the unit can be used to express many
other quantities. The dB is what scientists and engineers call a dimensionless
unit, meaning that it does not denote a fixed physical quantity. Instead, it indicates a logarithmic
ratio between any two quantities measured in the same physical units. In the case of
the bottle of wine, it means that the wine that’s "10dB better" tastes ten times
better than the previous one.
The Bel unit was developed by engineers at the Bell
Telephone Laboratories to quantify the signal loss over long distances of telephone cable
-- some sources say that the signal loss per mile of cable is 1 Bel. If the signal loss
over a given length of cable is 1 Bel, that means that the signal at the end of the cable
is 10-1, or 1/10 the signal at the beginning (as in accounting, losses are
negative). For smaller losses, it is more convenient to use the decibel (the prefix deci
means one tenth).
But just because 10dB is 10 times something, that
doesn’t mean that 2dB is 2 times something. That’s not how logarithms work. The
logarithm -- inverse power -- of 2 is approximately 0.3, so multiplying by 2 is a gain of
approximately 0.3 Bel, or 3dB. Similarly, multiplying by 4 is about 6dB. Going the other
way, halving a signal is -3dB, and quartering it is -6dB. Because the decibel is
logarithmic, successive gains or losses in signal can simply be added or subtracted. For
example, halving a signal (-3dB), then halving it again (-3dB), is equivalent to
quartering it (-6 dB). That convenience is what led to the widespread adoption of the
decibel in many industries.
Here’s the tricky bit: The equation for calculating
the decibel ratio of two quantities depends on the nature of those quantities. To express
a ratio of power levels in dB, one takes the logarithm of their ratio and multiplies the
result by 10. The difference for quantities such as voltage or pressure is that one takes
the logarithm of the square of their ratio or the ratio of their squares (the two are
mathematically identical). When you consider that power varies as the square of voltage,
that difference in calculation makes a lot of sense. What confuses many people is that
doubling a wattage measurement results in an increase of 3dB, but doubling a voltage
measurement results in an increase of 6dB.
Voltage gain
We’re all familiar with amplifiers being rated by
their maximum continuous output of power -- or, in the case of mass-market gear, by their
maximum conceivable output if the amplifier is struck by lightning. Many amplifiers,
particularly those marketed to the professional audio community, are also rated by voltage
gain. (Voltage gain is one of many measurements that we have done on all of the amplifiers
reviewed by the SoundStage! Network and listed at amplifiermeasurements.com.)
These specifications are usually given as dB. For example, you might see an amplifier with
a gain of 30dB. According to the equation explained above, that means that feeding the
amplifier a signal of 1 volt (V) will result in an output signal of about 31.62V. If you
insert a preamplifier with a gain of 12dB in front of the amplifier, you simply add the
individual voltage gains to get a total system voltage gain of 42dB. Now, when you feed
the preamplifier a signal of 1V, you’ll get 125.89V at the amplifier’s output.
(Actually, you probably won’t, as that would result in nearly 2000W being delivered
to an 8-ohm speaker. In practice, the input voltage of the preamp is limited, as is the
input voltage of the power amp.)
Sound power and sound pressure
For loudspeakers -- or any other source of sound -- there
are three different quantities that can be expressed in dB. The most intrinsic of these is
sound power, which is measured in watts (W). Sound power is the quantity of
acoustical energy produced by an object, and does not vary with distance: an object
producing 1W of sound power does so whether you stand 1m or 1km away from it.
A second, closely related quantity is sound intensity,
measured in watts per square meter. Sound intensity does vary with distance from
the sound source, since the same amount of energy is spread over a wider area. In order to
express these quantities as absolute measurements in dB, we need a reference point,
similar to the 1V we used above for voltage gain. The most common reference for sound
power is 10-12 watts (0.000000000001W) -- approximately the acoustic power of a
single mosquito on the wing. For comparison, the sound power of a jackhammer is 1W, or
120dB, in reference to the mosquito. The reference for sound intensity is 10-12
watt/m2.
The third quantity that relates to loudspeakers, and the
one with which most audiophiles are familiar, is sound pressure, which is measured
in Pascals. Sound pressure is the deviation from ambient pressure caused by a soundwave at
a particular point in space. It is the quantity to which our ears are sensitive, and which
is readily measured by a microphone. The reference level, in air, for sound pressure is
20µPa -- the pressure created 1m away from the previously cited mosquito, and the
smallest sound distinguishable by young, undamaged human ears. As with voltage, we
calculate dB values for sound pressure based on the square of the ratio of pressures.
The following graph shows the logarithmic nature of
decibels of sound pressure.
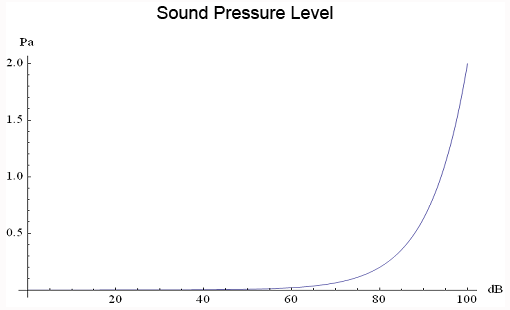
The minimum threshold for human hearing is 0dB. Some common
measurements of sound-pressure level (SPL) cited for real-world reference are: rustling
leaves, 10dB; a very quiet room, 30dB; normal conversation, 50-60dB; a major road from 10m
away, 80-90dB; and a jackhammer, 100dB.
The ear hears logarithmically. In other words, something
that is 80dB (SPL) sounds twice as loud as something that is 70dB (SPL), given the same
frequency content. Our ears don’t hear all frequencies equally well, so various
schemes have been developed to better represent human hearing. Any of these methods
involves assigning different weights to different frequencies that correspond with human
perception. The most common is A-weighting, often written "dBA." C-weighting
better represents how we hear loud or abrupt noises, and B- and D-weightings also exist.
Although speaker measurements are rarely expressed using these weighting schemes,
signal/noise ratio and even amplifier bandwidth sometimes are. It’s not crucial that
you understand how the frequencies are weighted, but you should recognize that dBA
doesn’t mean the same thing as dB, and that you can’t directly compare
two pieces of equipment whose manufacturers use different weightings.
Summing up
Now that you understand what a decibel is, you’ll have
a better idea of how to interpret audio specifications. And the next time somebody wants
to sell you a loudspeaker that’s "3dB more" than another one, ask him to be
more specific. Maybe he just means that it costs twice as much.
. . . S. Andrea Sundaram
|